Plot Lorenz Curve in Python
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
Gini coefficient, along with Lorenz curve, is a great way to show inequality in a series of values. However, there are no straight forward wrapper function to use for the plot. I’ve been using these a lot lately and woud like to write down how I do these with Numpy and Matplotlib.
Let’s first come up with a small sample set. To make a skewed dataset, I append two Poisson random samples together.
X = np.append(np.random.poisson(lam=10, size=40),
np.random.poisson(lam=100, size=10))
X
array([ 11, 11, 13, 10, 17, 14, 14, 9, 8, 11, 4, 13, 12,
9, 14, 11, 10, 11, 13, 17, 14, 6, 10, 8, 13, 14,
13, 5, 22, 8, 13, 10, 11, 14, 6, 6, 11, 10, 6,
7, 103, 86, 99, 94, 99, 95, 91, 95, 88, 79])
Calculation of Gini
The formula comes from Gini’s Wikipedia page:
Note that the values of $y$’s are ordered such that $y_i \leq y_{i+1}$
Now, we can write a simple wrapper function for this.
def gini(arr):
## first sort
sorted_arr = arr.copy()
sorted_arr.sort()
n = arr.size
coef_ = 2. / n
const_ = (n + 1.) / n
weighted_sum = sum([(i+1)*yi for i, yi in enumerate(sorted_arr)])
return coef_*weighted_sum/(sorted_arr.sum()) - const_
gini(X)
0.5305263157894735
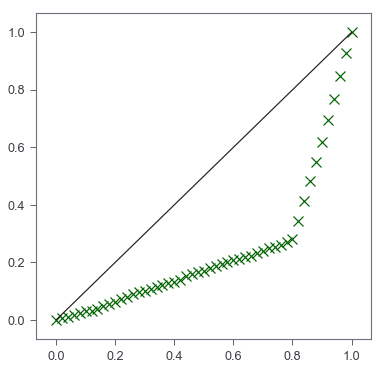
Lorenz Curve
There are two elements we need: perfect equality that has a slope of $1$ and the Lorenz curve.
Quote from Lorenz curve’s wiki page
The curve is a graph showing the proportion of overall income or wealth assumed by the bottom $x$% of the people
In fact, the famous 80-20 rule is one good example: the bottom 80% holds 20% of the overall wealth. Under the situation of perfect equality, on the other hand, we can say the bottom $x$% holds $x$% of the overall wealth.
Similar to Gini coefficient, we will sort the data. Then we convert values to cumulative proportions. We may also add the origin $(0,0)$
X_lorenz = X.cumsum() / X.sum()
X_lorenz = np.insert(X_lorenz, 0, 0)
X_lorenz[0], X_lorenz[-1]
(0.0, 1.0)
fig, ax = plt.subplots(figsize=[6,6])
## scatter plot of Lorenz curve
ax.scatter(np.arange(X_lorenz.size)/(X_lorenz.size-1), X_lorenz,
marker='x', color='darkgreen', s=100)
## line plot of equality
ax.plot([0,1], [0,1], color='k')
This gives us a very simple Lorenz curve. Then it is up to our own needs to add any customization.
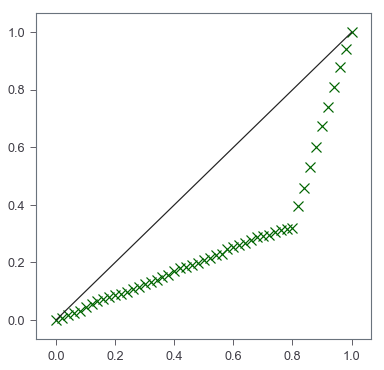
A wrapper function
def lorenz_curve(X):
X_lorenz = X.cumsum() / X.sum()
X_lorenz = np.insert(X_lorenz, 0, 0)
X_lorenz[0], X_lorenz[-1]
fig, ax = plt.subplots(figsize=[6,6])
## scatter plot of Lorenz curve
ax.scatter(np.arange(X_lorenz.size)/(X_lorenz.size-1), X_lorenz,
marker='x', color='darkgreen', s=100)
## line plot of equality
ax.plot([0,1], [0,1], color='k')
X = np.append(np.random.poisson(lam=10, size=40),
np.random.poisson(lam=100, size=10))
gini(X)
0.5620936639118459
lorenz_curve(X)